La matriz cuadrada es aquella que tiene el mismo número de renglones y columnas.
Ejemplo: Sean las matrices
Entonces, A y B son matrices cuadradas de orden 3 y 2 respectivamente.
MATRIZ TRIANGULAR SUPERIOR
En una matriz triangular superior los elementos situados por debajo de la diagonal principal son ceros.
MATRIZ TRIANGULAR INFERIOR
MATRIZ DIAGONAL
En una matriz diagonal todos los elementos situados por encima y por debajo de la diagonal principal son nulos.
MATRIZ DIAGONAL
Es una matriz diagonal en la que los elementos de la diagonal principal son iguales.
MATRIZ IDENTIDAD
Una matriz identidad es una matriz diagonal en la que los elementos de la diagonal principal son iguales a 1.
Matriz nilpotente
Matriz idempotente
Es una matriz diagonal en la que los elementos de la diagonal principal son iguales.
MATRIZ IDENTIDAD
Una matriz identidad es una matriz diagonal en la que los elementos de la diagonal principal son iguales a 1.
Matriz nilpotente
Una matriz NєMn,n(K) se dice nilpotente si existe kєN tal que NK=0.
Matriz idempotente
Una matriz A, es idempotente si A2=A
Matriz Involutiva
Una matriz A, es involutiva si A2=I, donde I es la matriz identidad.
Matriz traspuesta
Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas.
Por ejemplo:

Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas.
Por ejemplo:

Matriz simétrica
Una matriz simétrica es una matriz cuadrada que verifica

Una matriz simétrica es una matriz cuadrada que verifica
A=At

En la matriz simétrica tanto arriba como abajo de la diagonal principal, los elementos son iguales.
Matriz antisimétrica
Es una matriz cuadrada que verifica

Es una matriz cuadrada que verifica
A=-At.
Por ejemplo: En la matriz antisimétrica existe una diagonal principal de ceros, por debajo de la diagonal los elementos son positivos, y por encima de la diagonal los elementos son negativos.

Matriz Compleja
Cuando una matriz A está definida sobre el campo de los complejos.
Suma de una matriz real y una matriz imaginaria.
matriz A + i*matriz B
donde la matriz A está formada por números reales y el término i*matriz B formada por números complejos.
Por ejemplo:
Cuando una matriz A está definida sobre el campo de los complejos.
Suma de una matriz real y una matriz imaginaria.
matriz A + i*matriz B
donde la matriz A está formada por números reales y el término i*matriz B formada por números complejos.
Por ejemplo:
Matriz conjugada
Contiene a los conjugados de una matriz compleja, es decir la parte imaginaria de los elementos de la matriz cambian su signo.
Por ejemplo:
Contiene a los conjugados de una matriz compleja, es decir la parte imaginaria de los elementos de la matriz cambian su signo.
Por ejemplo:
Matriz Hermitiana
Es una matriz compleja con la característica de que su traspuesta conjugada es igual a ella.
Es una matriz compleja con la característica de que su traspuesta conjugada es igual a ella.
Matriz antihermitiana
Es aquella para la que la traspuesta conjugada es igual a menos la matriz original.

Es aquella para la que la traspuesta conjugada es igual a menos la matriz original.

Matriz ortogonal
Es aquella para la que se cumple que la matriz original multiplicada por su traspuesta es igual a la matriz de identidad.



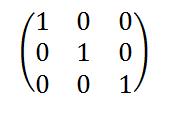







WOW
ResponderEliminar