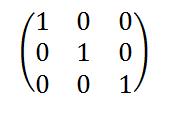En esta ocasión me acerque al Ing. Lucio Varela con la intención de conocer más a fondo las aplicaciones de los temas vistos en la unidad 3 y unidad 4 del curso de Matemáticas IV.
Para ello, le realice 4 preguntas, a las que contestó lo siguiente:
1. ¿Los temas de la unidad 3 tienen relación con otras asignaturas de la retícula de Ingeniería Industrial?
Ing. Varela: "Se aplica para modelos de optimización (maximizar utilidades o ingresos), investigación de de operaciones (en el simple primar y simple revisado), esa misma modelación se utiliza para la planeación y programación de la producción en Administración de Operaciones I y II"
2. ¿Los temas de la unidad 4 tienen relación con otras asignaturas de la retícula de Ingeniería Industrial?
Ing. Varela: "Ecuaciones diferenciales, específicamente se aplica en la modelación de programación no lineal(inventarios) y física II"
3. ¿Usted ha hecho uso de los temas de la unidad 3 y unidad 4 dentro del campo laboral?
Ing. Varela: "Si, en la modelación de optimización, la he aplicado para la mezcla de productos en programación de la producción, presupuestos de mano de obra directa e indirecta y en la evaluación de proyectos de inversión."
4. ¿Es indispensable para un ingeniero industrial tener conocimiento en cuanto a matrices y espacios vectoriales para desenvolverse laboralmente?
Ing. Varela: "Todo ingeniero debe desarrollar sus habilidades de la lógica matemática en la solución de los problemas derivados en su ámbito de su ejercicio profesional. sin embargo, lo más importante de las Matemáticas es desarrollar el hábito de actuar en todo momento metódicamente y sistemáticamente enfocándose básicamente en los detalles ante cualquier situación. Comportamiento y Cultura.
Adriana Gutierrez
sábado, 13 de noviembre de 2010
TIPOS DE MATRICES
MATRIZ CUADRADA
La matriz cuadrada es aquella que tiene el mismo número de renglones y columnas.

La matriz cuadrada es aquella que tiene el mismo número de renglones y columnas.
Ejemplo: Sean las matrices
Entonces, A y B son matrices cuadradas de orden 3 y 2 respectivamente.
MATRIZ TRIANGULAR SUPERIOR
En una matriz triangular superior los elementos situados por debajo de la diagonal principal son ceros.
MATRIZ TRIANGULAR INFERIOR
MATRIZ DIAGONAL
En una matriz diagonal todos los elementos situados por encima y por debajo de la diagonal principal son nulos.
MATRIZ DIAGONAL
Es una matriz diagonal en la que los elementos de la diagonal principal son iguales.
MATRIZ IDENTIDAD
Una matriz identidad es una matriz diagonal en la que los elementos de la diagonal principal son iguales a 1.
Matriz nilpotente
Matriz idempotente
Es una matriz diagonal en la que los elementos de la diagonal principal son iguales.
MATRIZ IDENTIDAD
Una matriz identidad es una matriz diagonal en la que los elementos de la diagonal principal son iguales a 1.
Matriz nilpotente
Una matriz NєMn,n(K) se dice nilpotente si existe kєN tal que NK=0.
Matriz idempotente
Una matriz A, es idempotente si A2=A
Matriz Involutiva
Una matriz A, es involutiva si A2=I, donde I es la matriz identidad.
Matriz traspuesta
Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas.
Por ejemplo:

Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas.
Por ejemplo:

Matriz simétrica
Una matriz simétrica es una matriz cuadrada que verifica

Una matriz simétrica es una matriz cuadrada que verifica
A=At

En la matriz simétrica tanto arriba como abajo de la diagonal principal, los elementos son iguales.
Matriz antisimétrica
Es una matriz cuadrada que verifica

Es una matriz cuadrada que verifica
A=-At.
Por ejemplo: En la matriz antisimétrica existe una diagonal principal de ceros, por debajo de la diagonal los elementos son positivos, y por encima de la diagonal los elementos son negativos.

Matriz Compleja
Cuando una matriz A está definida sobre el campo de los complejos.
Suma de una matriz real y una matriz imaginaria.
matriz A + i*matriz B
donde la matriz A está formada por números reales y el término i*matriz B formada por números complejos.
Por ejemplo:
Cuando una matriz A está definida sobre el campo de los complejos.
Suma de una matriz real y una matriz imaginaria.
matriz A + i*matriz B
donde la matriz A está formada por números reales y el término i*matriz B formada por números complejos.
Por ejemplo:
Matriz conjugada
Contiene a los conjugados de una matriz compleja, es decir la parte imaginaria de los elementos de la matriz cambian su signo.
Por ejemplo:
Contiene a los conjugados de una matriz compleja, es decir la parte imaginaria de los elementos de la matriz cambian su signo.
Por ejemplo:
Matriz Hermitiana
Es una matriz compleja con la característica de que su traspuesta conjugada es igual a ella.
Es una matriz compleja con la característica de que su traspuesta conjugada es igual a ella.
Matriz antihermitiana
Es aquella para la que la traspuesta conjugada es igual a menos la matriz original.

Es aquella para la que la traspuesta conjugada es igual a menos la matriz original.

Matriz ortogonal
Es aquella para la que se cumple que la matriz original multiplicada por su traspuesta es igual a la matriz de identidad.domingo, 12 de septiembre de 2010
sábado, 11 de septiembre de 2010
Aplicaciones de los temas de Matemáticas IV
Para formar un conocimiento más amplio
de las aplicaciones de números
complejos y sistemas de ecuaciones lineales,
me di a la tarea de
entrevistar a tres de los profesores
de ingeniería industrial: IIQ Alejandro López Mendoza, América Ávila Hernández y Ma. del Rosario Lara Delfin.
Básicamente la entrevista contenía tres preguntas: 1. en la práctica profesional de un Ingeniero Industrial, ¿en qué se aplican los temas de las dos primeras unidades de Matemáticas IV?, 2. ¿Es indispensable para un Ingeniero Industrial tener conocimiento de números complejos y sistemas de ecuaciones lineales?, 3. ¿Tienen relación los temas de Matemáticas IV con alguna otra asignatura de Ingeniería Industrial?
En resumen concluí lo siguiente:
Los tres profesores coincidieron al decirme q los sistemas de ecuaciones lineales
son muy utilizados en ingeniería industrial, incluso se aplican en otras materias por ejemplo:
investigación de operaciones I y II, estadística, control estadístico del proceso, simulación, administración de operaciones I y II, calidad y diseño de experimentos.
El ingeniero Alejandro López Mendoza me platicó
acerca de su experiencia en el departamento de producción,
donde para planear la producción se manejaban
restricciones que se representaban con
ecuaciones lineales y se resolvían
con sistemas de ecuaciones,
por ejemplo:
cantidad de materias primas,
transportes, los envases,
la mano de obra, etc.
En cuanto a los números complejos, su utilización es limitada a problemas muy específicos y
un ingeniero industrial no ocupa números complejos tanto como un ingeniero en electrónica o en mecatrónica, sin embargo no deja de ser importante tener las bases, sobre todo si un ingeniero industrial se dedica a la investigación.
Firmas de los profesores de
que se llevó a cabo
la entrevista
Ma. del Rosario Lara Delfin
América Ávila Hernández
Alejandro López Mendoza
La geometría de un sistema de tres ecuaciones con tres incógnitas
Considerando el sistema de tres incógnitas:
ax + by + cz = d
ax + by + cz = d
ex + fy + gz = h
ix + ky + lz = m
En donde a, b, c, d, e, f, g, h, i, j, k, l, y m son constantes y al menos una de ellas en cada ecuación es diferente de cero.
Cada ecuación del sistema representa una ecuación de un plano. cada solución (x, y, z) al sistema de ecuaciones debe ser un punto en cada uno de los tres planos. existen las siguientes soluciones:
1. SOLUCIÓN ÚNICA: el sistema tiene una solución única, si los tres planos se cortan en un punto, que corresponde a la solución del sistema. tendremos lo que se muestra a continuación:
2. NÚMERO INFINITO DE SOLUCIONES:
a) Los tres planos se cortan en una recta.
b) Dos planos son coincidentes y el restante se corta en una recta.
a) Los planos se cortan de dos a dos.
c) Dos planos son paralelos y el restante los corta.

Suscribirse a:
Comentarios (Atom)